
If a given wavelength is used in higher orders, for example, from first to second order, it is considered that because the dispersion is doubled, so is the limiting resolution. In a monochromator in which there are ancillary optics such as plane or concave mirrors, lenses, etc., a linear increase in the limiting resolution may not occur. The reasons for this include:
Even if the Full Width Half Maximum is maintained, a degradation in line shape will often occur – the base of the peak usually broadens with consequent degradation of the percentage of available photons in the FWHM.
The longest possible wavelength (λmax1) an instrument will reach mechanically with a grating of a given groove density is determined by the limit of mechanical rotation of that grating. Consequently, in changing from an original groove density, n1, to a new groove density, n2, the new highest wavelength (λmax2) will be:
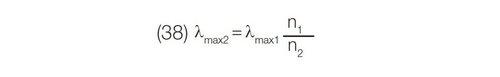
Table 6: Variation in Maximum Wavelength with Groove Density in a Typical Monochromator.
From Table 6 it is clear that if a 3600 g/mm grating is required to diffract light above 433 nm, the system will not permit it. If, however, a dispersion of 0.77 nm/mm is required to produce appropriate resolution at, say, 600 nm, a system should be acquired with 640 mm focal length (Equation (5)).
This would produce a dispersion of 0.77 nm/mm with a 2400 g/mm grating and also permit mechanical rotation up to 650 nm.
In Example 2, the solution to the dispersion problem could be solved by using a 2400 g/mm grating in a 640 mm focal length system. As dispersion varies with focal length (LB), groove density (n), and order (k); for a fixed LB at a given wavelength, the dispersion equation (Equation (5)) simplifies to:
(39) kn = constant
Therefore, if first order dispersion = 1.15 nm/mm with a 2400 g/mm grating, the same dispersion would be obtained with a 1200 g/mm grating in second order. Keeping in mind that kλ = constant for a given groove density, n, (Equation (9)), using second order with an 1800 g/mm grating to solve the last problem would not work because to find 600 nm in second order, it would be necessary to operate at 1200 nm in first order, when it has been shown in Table 6 that the maximum attainable first order wavelength is 867 nm.
However, if a dispersion of 0.77 nm/mm is necessary in the wavelength at 250 nm, this wavelength could be monitored at 500 nm in first order with the 1800 g/mm grating and obtain a second order dispersion of 0.75 nm/mm. In this case, any first order light at 500 nm would be superimposed on top of the 250 nm light (and vice-versa). Wavelength selective filters may then be used to eliminate the unwanted radiation.
The main disadvantages of this approach are that the grating efficiency would not be as great as an optimized first order grating and order-sorting filters are typically inefficient. If a classically ruled grating is employed, ghosts and stray light will increase as the square of the order.
Do you have any questions or requests? Use this form to contact our specialists.